qakrot.blogg.se - Data analysis toolpak excel 2016 to calculate mean

#Data analysis toolpak excel 2016 to calculate mean how to

Again, drag and select the range of cells that are part of your sample data and close the bracket for the COUNT formula. So, type COUNT( after what you already have in your formula bar. For this, you need to use the COUNT function. Your formula bar will now have the formula: =STDEV(B2:B14)/SQRT( To find the square root of a number, we use the SQRT formula.So your formula so far is: =STDEV(B2:B14)/ Click on the formula bar after the closing brackets of the STDEV formula and add a ‘/’ symbol to indicate that you want to divide the result of the STDEV function. Next, we want to divide this Standard deviation by the square root of the sample size.So far, you have used the STDEV function to find the Standard deviation of your sample data. Close the bracket for the STDEV formula.So, if your sample data is in cells B2 to B14, you will see: =STDEV(B2:B14 in the formula bar. This will add the location of the range in your formula.

Drag and select the range of cells that are part of your sample data.

Type the symbol ‘=’ in the formula bar.

Click on the cell where you want the Standard Error to appear and click on the formula bar next to the fx symbol just below your toolbar.

However, you could use the above formula to easily and quickly calculate the standard error. Unfortunately, unlike the Standard Deviation, Excel does not have a built-in formula to calculate the Standard Error, at least not at the time of writing this tutorial.

#Data analysis toolpak excel 2016 to calculate mean how to

How to Find the Standard Error in Excel Using a Formula

σ represents the Standard deviation of the sample.

The Standard Error for a sample is usually calculated using the formula: It also helps analyze the amount of dispersion or variation between your different data samples. This helps analyze how accurately your sample’s mean represents the true population. In other words, the standard error of a sample is its standard deviation from the population mean. The standard error of a sample tells how accurate its mean is in terms of the true population mean. So we usually take random samples from the population and work with them. When working with real-world data, it is often not possible to work with data of the entire population.

How to Find the Standard Error in Excel Using the Data Analysis Toolpak.

How to Find the Standard Error in Excel Using a Formula.

Confidence Level (95%): The interval around the mean where you can be sure with 95-percent probability that the interval contains the actual mean.

Maximum: The highest value in the data set - 1,066, or 17.77 minutes per mile.

Minimum: The lowest value in the data set - 399, which is 6.65 minutes per mile.

Range: The difference between the lowest and highest values - 667 seconds, or about 11.1 minutes.

The skewness for a normal distribution is 0.

Skewness: Indicates whether the data is symmetrical when plotted compared to a normal distribution.

The kurtosis for a normal distribution is 3.

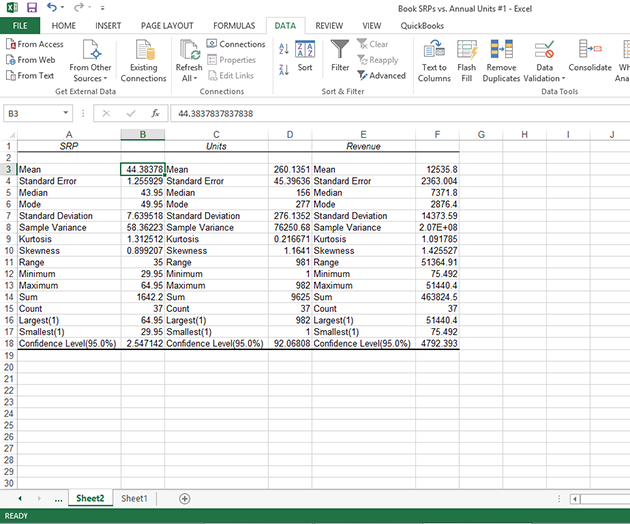
Kurtosis: Indicates whether the data is peaked or flat when plotted compared to a normal distribution.Standard Deviation: An indication of how widely dispersed the numbers are around the mean.Mode: Most common value - 675 seconds, or 11.25 minutes per mile.Median: Middle value - here, 697 seconds, which is about 11.6 minutes per mile.In a normal distribution, almost all values will be within three standard errors of the mean about 95 percent will be within two standard errors and about two-thirds will be within one standard error around the mean. Standard Error: This is how close your sample values are to the mean.Mean: Average value - here, that would be 716.69 seconds, or almost 12 minutes per mile.